前言

今天刷leetcode的时候，使用的其中一个解法出现了精度问题。代码如下：

/**
 * @param {number[]} digits
 * @return {number[]}
 */
var plusOne = function(digits) {
   // 将数组转换成字符串再通过Number转换成数字并加1，最后转成字符串
   var str = Number(digits.join("")) + 1 + "";
   // 将字符串转成数组
   digits = str.split("");
   // 通过遍历数组将每个元素转换成数字
   digits.forEach(function (val,index) {
       digits[index] = Number(digits[index]);
   });

   return digits;
};

上述代码目的实现：一个非负整数组成的非空数组（最高位在首位，且不为0），在该数的基础上加一，返回一个新的数组，数组中每个元素只存储一个数字。某一测试用例：

输入：
[6,1,4,5,3,9,0,1,9,5,1,8,6,7,0,5,5,4,3]
输出：
[6,1,4,5,3,9,0,1,9,5,1,8,6,7,0,5,0,0,0]
预期：
[6,1,4,5,3,9,0,1,9,5,1,8,6,7,0,5,5,4,4]

以上不难发现，在将字符串转换成数字的时候丢失了精度。

Number 类型

Js 中的数字类型只有 Number 一种，它采用 IEEE754 标准中的 “双精度浮点数” 来表示一个数字，并且不区分整数和浮点数。

存储格式

在 IEEE754 中，双精度浮点数采用 64 位存储，即 8 个字节表示一个浮点数。其存储结构如图：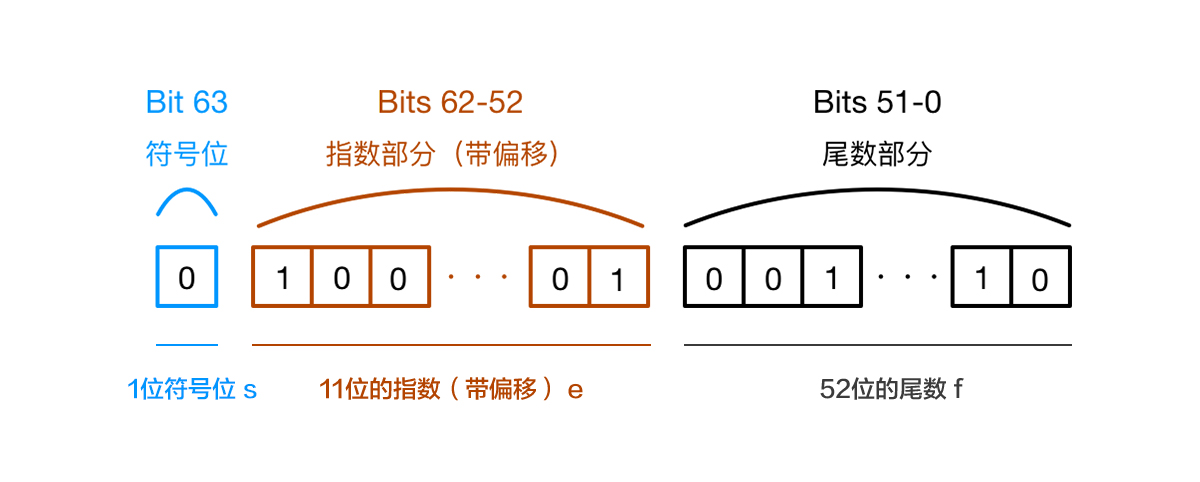

第0位：符号位，s 表示，0表示正数，1表示负数；
第1位到第11位：储存指数部分，e 表示；
第12位到第63位：储存小数部分（即有效数字)，f 表示；

数值精度

在 64 位的二进制中，符号位决定了一个数的正负，指数部分决定了数值的大小，小数部分决定了数值的精度。

IEEE754 规定，有效数字第一位默认总是1。因此，在表示精度的位数前面，还存在一个 “隐藏位”，固定为 1 ，但它不保存在 64 位浮点数之中。也就是说，有效数字总是 1.xx…xx 的形式，其中 xx..xx 的部分保存在 64 位浮点数之中，最长为52位。
所以，Js 提供的有效数字最长为 53 个二进制位，其内部实际的表现形式为：

(-1)^符号位 1.xx…xx 2^指数位

这意味着，Js 能表示并进行精确算术运算的整数范围为：[-2^53 -1，2^53 -1]，即从最小值 -9007199254740991 到最大值 9007199254740991 之间的范围。

在 Js 可以通过如下代码获得：

Number.MAX_SAFE_INTEGER = 2^53 - 1 = 9007199254740991 
Number.MIN_SAFE_INTEGER = -(2^53 - 1) = -9007199254740991

对于超过这个范围的整数，Js 依旧可以进行运算，但却不保证运算结果的精度(开头的例子明显超出了这个范围)，不仅是 Js，其他采用了 IEEE745 浮点数表示法，都会存在这个问题。

精度丢失过程

计算机中的数字都是以二进制存储的，如果要计算 0.1 + 0.2 的结果，计算机会先把 0.1 和 0.2 分别转化成二进制，然后相加，最后再把相加得到的结果转为十进制。

但有一些浮点数在转化为二进制时，会出现无限循环。比如，十进制的 0.1 转化为二进制，会得到如下结果：

0.0001 1001 1001 1001 1001 1001 1001 1001 …（1001无限循环）

而存储结构中的尾数部分最多只能表示 53 位。为了能表示 0.1，只能模仿十进制进行四舍五入了，但二进制只有 0 和 1，于是变为 0 舍 1 入。因此，0.1 在计算机里的二进制表示形式如下：

0.0001100110011001100110011001100110011001100110011001101

用标准计数法表示 0.1 + 0.2 的过程：

因此 0.1 + 0.2 = 0.30000000000000004

如此看来，我们在 Js 中的浮点数四则运算，其实是不精准的。

四则运算

关于Js四则运算，大家可以翻阅《Js高级程序设计》操作符的详细介绍，我在这里要说明的是，涉及金额（浮点数）计算时，我们的处理方法：

/**
 *两数相加
    *@param {float} a 加数1
    *@param {float} b 被加数2
    *@return {float} 返回两数相加结果
    **/
add: function (a, b) {
    if (typeof a == "undefined" || typeof b == "undefined" || a==null || b== null) {
        return NaN;
    }
    var c = 0;
    var d = 0;
    var e = 1;
    try {
        c = a.toString().split(".")[1].length;
    } catch (f) { }
    try {
        d = b.toString().split(".")[1].length;
    } catch (f) { }
    return e = Math.pow(10, Math.max(c, d)), (this.mul(a, e) + this.mul(b, e)) / e;
},

/**
 *两数相减
    *@param {float} a 减数1
    *@param {float} b 被减数2
    *@return {float} 返回相减结果
    **/
sub: function (a, b) {
    if (typeof a == "undefined" || typeof b == "undefined" || a==null || b== null) {
        return NaN;
    }
    var c = 0;
    var d = 0;
    var e = 1;
    try {
        c = a.toString().split(".")[1].length;
    } catch (f) { }
    try {
        d = b.toString().split(".")[1].length;
    } catch (f) { }
    return e = Math.pow(10, Math.max(c, d)), (this.mul(a, e) - this.mul(b, e)) / e;
},

/**
 *两数相乘
    *@param {float} a 乘数1
    *@param {float} b 乘减数2
    *@return {float} 返回两数相乘结果
    **/
mul: function (a, b) {
    if (typeof a == "undefined" || typeof b == "undefined" || a==null || b== null) {
        return NaN;
    }
    var c = 0;
    var d = a.toString();
    var e = b.toString();
    try {
        c += d.split(".")[1].length;
    } catch (f) { }
    try {
        c += e.split(".")[1].length;
    } catch (f) { }
    return Number(d.replace(".", "")) * Number(e.replace(".", "")) / Math.pow(10, c);
},

/**
 *两数相除
    *@param {float} a 乘除1
    *@param {float} b 乘除数2
    *@return {float} 返回相除结果
    **/
div: function (a, b) {
    if (typeof a == "undefined" || typeof b == "undefined" || a==null || b== null) {
        return NaN;
    }
    var c = 1;
    var d = 1;
    var e = 0;
    var f = 0;
    try {
        e = a.toString().split(".")[1].length;
    } catch (g) { }
    try {
        f = b.toString().split(".")[1].length;
    } catch (g) { }
    return c = Number(a.toString().replace(".", "")), d = Number(b.toString().replace(".", "")), this.mul(c / d, Math.pow(10, f - e));
},

分析：

1.乘法mul，思路是两个乘数都拿掉小数点，使用整数进行计算，最后再除以10^(扩大的倍数)，例如mul(5.5,8.0),实质通过函数转换成：55 * 8 / 100;
2.加法add，思路是将两个数通过mul拿掉小数点，然后再缩小相应的倍数。例如add(10.12,8.39)，实质是
(mul(10.12,100) + mul(8.39,100)) / 100
3.减法sub原理同add。
4.除法div，思路是将除数与被除数拿掉小数点，然后相除，最后乘以10^(-扩大的倍数)

以上大家可能比较疑惑的就是return语句中的逗号操作符，我查阅过Js高程、Js权威指南、Mdn，都描述得很简单，最后是在一些博客中找到些零散的点。总结如下：
1.逗号操作符在所有操作符中优先级最低。
2.return x, y, z 会返回最右边的值。
3.return e = 1, y 中由于 , 优先级低于 = 所以会先进行赋值操作，语句等价于 return e, y 也是返回y，不同的是返回y的时候，e已经赋值过了。
4.alert(x,y,z) 由于alert只接受一个参数，所以会忽略 y和z 两个参数，直接alert(x);
5.alert((x,y,z)) 会alert(z)。

参考文章

0.1 + 0.2 = 0.30000000000000004 该怎样理解？
IEEE754 浮点数格式与 Javascript number 的特性